演算法筆記
05 February 2021
演算法本質
- 設計出一套邏輯或者解決方法(能越general越好),在遇到類似的問題時能套用這個方法有效解決(速度快、需要空間少)
- 設計一套演算法需要注意
- 定義問題,最好能把給予的情境的問題變成一個general的問題
- 設計演算法解決他
- prove correctness (通常使用反證法)
- 假設演算法是錯誤的,但最後推論的到矛盾結果
- 假設演算法不是最佳解,有更好解法,但推論出他的結果不比我們的演算法好
- time / space analysis
如何衡量演算法的好壞
- 通常藉由時間複雜度或空間複雜度衡量
- 要能夠精確衡量需要多少的instructions, 多少的運算是非常困難也非常耗時間,而且CP值不高,我們更需要的是一個能夠快速、但不用那麼精確衡量演算法的方法(總不能每次想到一個新的演算法或想法就要花上數個月的時間來計算他的好壞,我們偏向有一個粗略的做法大致上快速衡量他到底可不可行、好不好)
- 我們通常不在意數值小的情況,現在電腦很強,小的數值不同演算法不會有太明顯的差異,我們要在意的適當數值大的狀況下的表現(當然當數值很小的時候,我們根本 用什麼演算法就都沒差)
- 因此我們以演算法在數值大的狀況下他所花的資源、時間的趨勢來判斷、比較演算法的好壞
- 我們使用O(n)之類的方式來判斷,雖然不精確能夠判斷他所需要的時間跟運算數量(就算同屬O(n),時間上也可能有些差距),但這粗略的方式能夠幫助我們快速衡量
- 考慮的量級單位為輸入的bit數量或者輸入的數字量
O(g(n)) -> 存在一個c, n0 such that f(n) <= c*g(n) , for all n > n0
o(g(n)) -> for all positive c,存在 n0 such that f(n) < c*g(n) , for all n > n0
DP
- 子問題要overlap,重點是定義substructure,然後就是不斷地位解,每個substructure就是有一些參數不同(e.g. 01背包就是物品跟重量),跟一個value(output)
- DP最終解是optimal,則切成的子問題也要是optimal
- 要證明問題的optimal解是由optimal substructure組成
- rod cutting, knapsack (0/1, 可重複取), LCS, weighted interval schedule
- 寫出遞迴式 F(n) = F(n-1)….
- 可以有space-efficient的寫法, 例如跑button up時不用記錄所有行數,只記錄目前所在的行數跟前面一行用到的就行,或者DP+DC, 把問題切成數個non-overlap問題在最後比大小,這樣也可以有效減少空間(e.g. optimize path時,例如確定一定要經過某行,對那行做DC)
把大問題切成子問題遞迴下去並把子問題答案記下來,之後要用到直接讀答案 例如knapsack就考慮取與不取這個物品得到兩個子問題(取跟不取, 子問題就是Weight跟item set不同)
Backtrace都是由終點往最小的值的方向走
DC
- 適用於可以把問題切成多個獨立、一樣的問題時,且base problem非常trivial時,而且合併不會花太多時間(O(n))
- 問題切成多個獨立的subproblem, 一個一個計算並且combine
- Recurrent Tree, substitution, Master Theroem來計算
- combine是O(n) 基本上合起來也會是O(nlogn)
- 先想base case, 找出幾個base case的規律後寫出簡單規則,在驗證稍微複雜一點的會不會work,並作修正
Examples:
- Merge sort T(n) = T(n/2) + O(n)
- Maximum Subarray O(nlogn)
- Divide into two subarray recursively
- Combine check lefmax, rightmax, max(middle)
- max(middle): leftmax which include the mid point + right max include the mid point
- Kadane algorithm(DP method faster)
- closest pair of point
- 矩陣乘法 (切成多塊小矩陣,只是還是O(n^3))
- parity check (檢查有奇數還偶數個bit 1)
- 把8個bytes的int切成兩個4個byte互相xor,結果為0的bit代表那個位置有偶數的1(0 or 2),結果為1的代表那個位置有奇數個bit 1
Reference
Time Complexity calculation

記得O(n)代表的是長期演算法的趨勢,所以我們在乎的是在某個n之後都會被bound住
- DC formula: T(n) = aT(n/b) + C(n)
- Substitution method: Guess the form of solution (e.g. T(n) = O(n^2)), use mathematical induction to prove it correct
- 可以用替換變數、減去更小次方的變數來幫助證明
- Recurrsion tree
- 不斷遞迴表示下去,node可以改成n項,最後加起來
- 大師法
- 用於aT(n/b) + f(n)
- 也適用recursion tree證明
- 看logb(a)和f(n)的成長速度的關係,logb(a)決定有幾個f(n)
Greedy
- 因為做了某個最佳的選擇後切成subproblem
- 證明部分分成兩個部分證明(證明greedy choice property跟optimal substructure)
- Greedy choice property: 如果有optimal solution, 證明greedy choice的選擇有包含在optimal solution裡
- 反證法, 假設optimal solution的選擇不包含這個greedy choice, 那把選擇改成greedy choice會更好或者不會更差
- Optimal substrcture: 證明完greedy choice property後, 這個選擇完會得到一個Subproblem, 證明這個subproblem的optimal solution也是包含在原本大問題的optimal solution裡
- 證明Greedy choice存在optimal解裡 (greedy choice的選擇會no worse than OPT solution)
- 反證法, 假設subproblem的optimal解不包含在大問題的optimal solution, 那證明subproblem的optimal解配合上我們的greedy choice能夠得到比原本大問題更好的optimal解, 證明了原本大問題的optimal解不是最佳解(矛盾), 證明所以小問題的optimal解也會包含在原本大問題的optimal解裡面
- Proof of Greedy choice property:
- 證明local optimal choice can lead to global optimal choice
- 反證假設存在OPT’不包含greedy choice, 證明把選擇改成OPT choice後不會比OPT’差
- 得證greedy choice在這個問題裡得到的解不會比OPT差
- Proof of Optimal Substructure
- 證明子問題用greedy choice也會得到是最佳解
- 反證法, 假設subproblem存在比OPT的greedy choice更好的解法OPT’ > OPT - 1(第一次選擇產生的subproblem), 則代表我採用OPT’的話得到的OPT’ +1 比OPT好, 可是我們上面證明greedy choice不會比OPT差,代表我們假設錯誤, 代表subproblem不存在比greedy choice更好的解法
- huffman code 可以用priority queue來寫, 每次pop出現機率最低的兩個字元建一個tree然後再把新的機率push回去priority queue
- 特化scheduling(not weighted)
- merkle hellman
Graph
Graph名詞解釋
Graph是由點(Vertex,Node)跟線(Edge)組成的一種圖
Directed graph: 有向圖, 每個edge只是單向連接
Undirected graph: 無向圖, u,v兩點間的edge可以從u走到v或v走到u
cycle: 繞一圈
Simple path: 除了起點、終點外,沒有任何一點經過兩次形成的path
Connected graph: 每個node都能走到其他所有node
connected Component: 在一個undirected graph裡,某個subgraph是connected,而且在加入任何的node, edge後,就沒辦法讓這個subgraph維持connected graph, 這樣的一個subgraph為connected component(所以基本上在undirected graph裡,一個graph就是他本身的connected component,因為他沒有方向,一定都互通)
strongly connected component: 在directed graph, 存在一個subgraph使這個subgraph內任兩點都能互相走到彼此, 且增加任何一個vertex,edge會讓他失去connected graph的特性
Self loop: edge的起點跟終點是同一個node
multigraph: 某兩個vertex中間有多個edge連接
Degree: 一個node對外連接的edge數
Forest: acyclic, undirected graph
Graph representation: adjacency list or adjacency matrix
Reference: alrightchiu.gitub.io
Adjacency List
suitable for sparse graph
檢查u,v是否相連: O(degree(u)) (把u的adjacencylist爬完)
把所有edge印出來Theta(V+E)
適用於列出一個node的所有outgoing node
space: theta(E+V)
Time to check an edge: theta(degree(u))
Time to list all neighbors: theta(degree(u)), for undirected graph
Time to list all edges: theta(E+V)
adjacency matrix
suitable for desnse graph
space: theta(v^2)
Time: check if (u,v) exist: theta(1)
Time: list all neighbors of u: theta(V)
Time: identify all edges theta(V^2)
適用於要快速確認某兩個node之間是否有edge, 列出一個node的所有incoming node
Tree
full binary tree & Complete binary tree
Tree:
- acyclic, connected undirected graph
- 任兩個node之間的path只有一條
- 如果再tree裡在加任一條edge, 會行成cycle
- 如果移除tree上任一條edge, 那此graph就不是connected graph
Binary tree: 一個tree他的internal node只有一或兩個children
Full(proper) binary tree: internal node一定是0或2個children且所有leaf node都是同個depth, 但不一定要從左填到右, 可以右邊的internal node有leaf但左邊的沒有, external node一定比internal node多一個, 所以只要有left child的話一定會有right child, 不用擔心只有一個child的狀況
Complete binary tree: 按照full binary tree建造的tree, 但可能沒建造完(例如最後一個internal node只有一個leaf node, 再多一個node才會變成full binary tree), 定義是所有除了最後一個level的node都填完的tree, 而且最後一層要從左填到右
binary tree的種類, 可以是full binary tree也可以是非常不平衡的tree都往左邊長, 導致height = node數量, external node=1, 而full binary tree則是external node = internal node+1, external node = 2^height
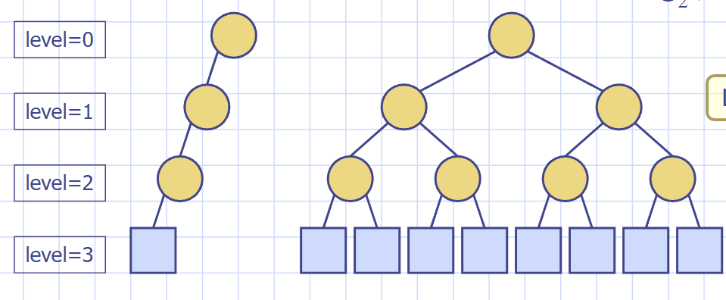
traversal四種不同traversal: inorder(在bst中會是sort後的序列), preorder(不等於bfs, level order的方式), postorder(在arithmatic tree常用), level order(bfs,用queue實做)
找inorder successor:
- case1:
- 該node有right child, 那就先移到right child後找leftmost node就是successor
- case2:
- 該node沒有right child, 那就要往上找, 如果自己這個node是parent的left child的話 就一樣右移到right child後找到leftmost node
找inorder predecessor(把上述概念左右對調即可):
- case1:
- 該node有left child, 移到left child後找到rightmost node
- case2:
- 該node沒有left child, 上移到parent直到cur node是parent node的right child, 那就一樣左移到left child後找到rightmost node
Binary serach tree deletion:
if curnode is the delete target
if right node == NULL:
return left child //如果沒有右子樹, 回傳左子樹,左子樹是NULL就代表是leaf node
else:
find curnode右子樹subtree的successor
return successor/predecessor
else:
curnode->left = dfs(curnode->left);
curnode->right = dfs(curnode->right);
return curnode
當然上述的內容也可以左右對調,變成找left subtree的predecessor, 那上述演算法的right/left就都要對調
Graph BFS
Input: Graph
Output: 每個reachable node跟他和start point的距離
Time COmplexity: O(V+E)
做法: 利用queue來做BFS(要記錄走過的點), 首先先對每個node做initialize把它距離設成無限
可以記錄的資訊包括,每個node跟start node的距離、每個node的predecessor,node是否走過。在做bfs or dfs時,要加一個參數來記錄這個node是否在queue裡面(白色代表未走過、灰色代表已經在queue內、黑色代表已經走完pop出queue了),不然很有可能重複走node或者把他push進queue兩次以上
O(V+E): V for initialization, E for traverse
BFS Tree: BFS traverse完後得到connected的graph, BFS tree並不唯一, 另如某兩個點到一個新的點的距離是一樣的, 那最後會時由哪個點走到新的點是由adjacency list上面的node順序做決定 BFS Forest: 找出各個connected graph, 只要是還沒走過的node, 就對她做一次Graph BFS 得到一個新的BFS Tree
可以用來找connected components of undirected graph BFS只能做undirected graph裡的cycle detection, directed graph的作法如下
Find if a graph is SCC with BFS 基本想法:跑BFS紀錄走過的點,接著reverse graph再跑BFS一次, 檢查兩次走過的點是否相同
DFS
- Finding connected component, strongly connected components
- topological sort(紀錄每個節點return時的cnt,cnt按照由大到小排序)
- DAG/cycle detection(檢查一個graph是否為Directed Acyclic graph, 紀錄discover跟End time, 當某次dfs走到的點為有discover但沒有end time時, 代表有cycle)
- 做cycle detection, visited的array要有三個狀態(node in current path, non-visited, visited),在directed graph裡, 如果造訪的某個node是visited, 那他不一定是cycle, 要是造訪的node是在current path才會是cycle
- edge type
- tree edge: 單純A連到B,B沒走過時這種就是tree edge
- back edge: 當連到的點已經走過的時候,例如在DFS時A連到B,但發現B已經走過了。有backedge代表這個graph是cyclic
topological sort(DAG才有意義): 要確保指向別人的會先做, 被指到的最後做, 所以DFS finish time遞減可以保證指向別人的先做,然後就算一個點指向多個點, 也會是root node先做, 另一種狀況是一個點被指到很多次, 那就要所有指向他的點先做(DFS finish time也行),DFS紀錄Finish time, Finish time由大到小就是topological order, 所以紀錄順序方法之一就是把node變成finish node時順便push進stack,然後結束dfs後把stack pop出來就是topological order
time complexity: Theta(V+E)
Set operation
在一個undirected graph裡面找到connected components, 找到後是否能夠快速確認兩個node是否在同個connected component? 或者我們能不能夠簡單的判斷新增一條edge會把哪些connected component變成一個大的connected component
- 可以利用dfs, bfs找出從某個root點出發能夠到達的所有點
- setcollapsing, 對於走到的點,都把他連回出發點root, 所以會變成一個兩層的tree, root有很多的leave, 每個leave代表root能到達的點
- 除了用graph外,也可以用array, array index代表該node, index裡面的值代表他指向的node,所以上述例子,leave的index value都是root的value,而root的index value就是自己,這樣要查找兩個node是否是在同個connected graph只要查找array表是否連到同個root
- 當要合併兩個connected graph時,好的做法是把數量少的graph接到數量大的graph的root下面
如果今天無法用array,那就要更改原本的graph, 如果改graph不是好選擇,可以考慮用C++ map或set實作
Minimum Spanning Tree
Spanning tree: subgraph that is a tree and connect all the vertices
minimum spanning tree: weighted graph找到最小的weight sum讓所有點相連
MST is unique 如果每個edge的weight都不同(proof by contradiction, 假設有兩個mst, 因為mst再新增任何一個邊會有cycle, 就可以在一掉其中一個邊, 讓mstb == msta)
Kruskal algorithm
Kruskal algorithm: 有點像greedy,每次選最小的那個邊並確保不會產生cycle -> O(ElogV) 先把每個點都弄成一個set(或者node多一個變數記錄他的group,每次連接就把新的node變成同個group, set operation),接著從最小edge開始找, 看連接兩端的node是否在同一個set,不是的話就union起來
Make-Set: O(1)
Find-Set: O(logV)
Union: O(logV)
Sort Edge: O(ElogE) = O(ElogV), 因為V個點最多V^2個邊, O(ElogV^2) = O(2ElogV)
所以整體複雜度sort edge加上對每個edge進行連接兩端的node的find-set, union運算: O(ElogE + E*2logv) = O(ElogV)
Proof of correctness
因為我們都是從最小的edge開始檢查, 所以當某個edge會產生cycle時,代表這個edge是目前連接的點中,最大的edge,然後把他加入會是一個不必要的edge,所以我們不要(Cycle property). 反之,如果加入某個edge會擴大目前的MST,代表這個edge是連接這個點中最小的edge,所以要加入(Cut property). 這個想法同時適用於kruskal, prim的證明
Prim algorithm
Prim’s algorithm: 從其中一個點開始然後greedy長成一棵樹(選擇weight最小的edge連接到isolated node) -> O(ElogV) 可以用min priority queue來存所有可以選擇的Edge並Pop出最小的那個
跟Dijkstra類似, 只是dijkstra是要找距離root node最近的點,而Prim是要找距離整棵樹的leaf node最近的點
1. 先把所有點initialize(所有點的distance設為無限大)並push進min heap, 起始點的distance設為0
2. pop min heap裡最小的點並relax跟他有連接的點的距離
3. 更新的點每個都要做decrease key, 即找到點的位置後更改distance做upheap
4. 重複2,3
或許也可以先選定起點, 把跟起點相鄰的edge push進heap裡, 每次pop heap中最小的edge出來 看能不能連到新點, 可以的話他就是MST其中一個edge, 然後再把新連到的點的外接的edge也都Push進heap裡. 然後就這樣不斷加新的邊, 複雜度為O(VlogE), 每次edge的pop是Log(E),然後我們要連接V個點,所以大約做個V次, 空間複雜度為O(E),
Min HEAP: O(V)
Extract Min: O(logV)
Decrease KEY: O(logV)
Running Time: O(ElogV + VlogV): ElogV是因為做decrase key為logV,然後每個edge都要做, VlogV為一開始建立min heap把所有node都放進去,每次要把一個pop出來值到empty,所以是VlogV
Cycle property: 如果有一個cycle在graph裡, 則cycle內weight最大的edge就不會再MST裡
Cut property: 如果graph把它cut成subgraph,則最小邊e一定在MST裡
用途: 當edge少時, 可以用kruskal 當node之間連接很複雜很多edge時, 可以用prim
build heap with sift down: O(n): link
Relaxing
relaxation, 通常在算MST或者shortest path, 處理一個點, 把它納進我們的set裡時,會更新到其他點的最短距離, 這個改變其他點的最短距離(例如從無限大改成v+d[u,v]這樣), 這個運算叫做relaxation. 例如現在有s,u,v三點, 納入v以後重新考慮s,u之間的距離(比較d(s,u)跟d(s,v)+d(v,u)的大小)
Strongly Connected Component
定義: SCC內每個點都一定有路徑能走道SCC內的其他任一點, Graph G和Graph G^T 有一樣的strongly connected component
- 跑DFS並把結束的點push到stack裡面
- 把graph transpose, 即graph edge方向相反(directed graph部分)
- 接著再把stack pop把node拿出來做DFS, 有連城cycle的話就是一個SCC,然後SCC內的點stack pop後就不用再做一次DFS
說明:
要能夠用DFS找SCC, 選擇起點非常重要, 最好是能夠不斷地每次找點都是從sink node(最少out connected的node)開始, 這樣找才能夠找到各個seperate的SCC. 不然如果開始的起點是找到某個點,而這個點會連到另一個SCC,那只做一次DFS要找到SCC難度就變得相對不容易. 所以我們要能夠確保能夠從sink node開始(finish time最小的), 就要做DFS然後依據finish time push到stack裡, 這樣就能知道sink node(sink node理論上都是被連到為主,所以絕對比非sink node早結束), 接著在reverse, 此時在stack top原本是最多外連的變成最多內連的.
Time Complexity
- 1st DFS: O(V+E) 建立topological sort
- Graph transpose: O(E)
- 2nd DFS: O(V+E): 從distance最大的地方開始做,如果最後能成為一個cycle就是SCC
Reference:
Shortest path
通常是考慮directed, weighted graph
跟MST有點不同是, MST是不會有given node而是要找到最小的Sum weight連接最多點, 但Shortest path通常是給定一個起點要去找他到其他點的距離, 所以可能在solution上有些狀況兩者會不同
shortest path可以包含negative weight但不能包含negative cycle
我們假這shortest path graph weight都大於0
- shortest path不一定是unique一條, 但一定是只有一個unique的weight值(最終路線的sum of weight)
-
一定找的到shortest path, given a graph
- shortest path tree: 一個graph G’(V’,E’)符合以下條件
- V’ 是原本graph G的subgraph的node, E’是graph G的sub edge
- G’是一個rooted tree
- G’內s到v的shortestpath跟G裡面s到v的shortest path相同
Shortest path in DAG
因為沒有cycle, 作法是利用topological sort的order來更新node的距離, 每次找indegree為0的node更新他到source的distance, 當然也可以用dijkstra
Dijkstra
- All edge is non-negative
- 維持一個set紀錄所有已經走過而且確定最短路徑的node
- 用greedy, 每次選擇一個沒走過的點(不再set裡面的點),而且此點是連接到目前set裡面的點的距離最短的
- 加入新的點後做node relaxation
- 跟Prim MST的差別在於, Prim MST再找距離樹的leaf最近的(weight最小)的node,Dijkstra是找距離root(start point)最短的node
- negative weight可能不會work(例如起點到某個點 要先經過一個距離正超大的點後在走一個距離負超大的點到,總和很小或者甚至是負數, 那另一條路徑是起點直接走一個小正數的邊到那個點,那這樣會是後者走到那個點而不是走極大的正數加上極小的負數那條路)
1. 先把所有node initialize,每個node的距離(u.d)設為無限大,然後起始點設為v.d = 0
2. 利用min heap先把起始點push進去
3. 把一個點從min heap pop出來, 開始做relaxation, 更新與v相連的點u的u.d
4. 有更新的點push進去min heap, 並重複第二步驟
Time Complexity:
# of insertion: O(V)
# of Extract-Min: O(V)
# of Decrease key: O(E)
如果用array來implment priority queue: O(V^2+E) (因為每次只加入一個點所以要做V次, 每次要iterate整個array(V)來找min node和relax,每個edge都要relax, 所以是E, 但這樣做法會有問題在於假設有negative weight那就極有可能得到錯的答案,原因如上所述, 所以如果有negative edge的話,最好解法還是用priority_queue在每次relax成功後都push該node進去, 時間複雜度為O(ElogE))
Reference: decrease key
Reference: Dijkstra implementation
基本上就是用priority_queue<pair<int,int» 的方式, 第一個元素紀錄起點到該點的distance, 第二個元素紀錄哪個node, 這樣compare時會先依據distance來做排序, 然後這種狀況下極有可能一個點被push進去priority_queue兩次, 就是多次relax都有更新某個node的距離, 但反正pq出來的一定都是最小的那個距離, 所以算完後此時該node會變成那個最短距離, 之後pq在pop出同一個node但是距離更大的狀況時, 他因為不會成功relax就不會有任何操作(就變成單純被pop出來) , 所以這種作法就是判斷pop出來的node有沒有要順利relax, 有的話才做update distance跟push進pq, 不然就不理他, 這樣也不用visited記錄該node是否visited, 但worst case就是每個edge都relax成功導致Space complexity是O(E), Time Complexity是O(ElogE)
Bellman Ford
- Edge can have negative weight
- Able to find negative weight cycle
- slower than Dijkstra
做法: 總共N個點,每次就對所有的邊做relax, 第一次只會做到跟s相連的edge, 第二次就會這樣延伸出去做relax, 有bfs的感覺,然後因為shortest path是optimal substructure, 所以我們這樣求得短的shortest path可以apply到長的(即很遠的點的shortest path就是由數個短的shortest path組成的). 因為只有n個點,理論上n-1次這樣的做法就應該要到達終點,求得起點到所有點的shortest path, 如果地N次iterate還有更新的話代表有negative cycle.
for i in range(V-1):
for edge(u,v) in G(V,E):
relax(u,v,w)
relax(u,v,w):
check u.d, v.d + w(u,v) 大小比較 // u.d, v.d為u,v到s的距離
Time Complexity: O(VE) = O(V^3), loop V次,每次relax所有Edge(如果graph用matrix存,那就是V^2)
Proof of Correctness:
如果(u,r)的shortest path有經過v, 則(u,v)的shortest path就是(u,r)的這個片段 (反證法) 每次relax一條邉連到新的點, 不斷這樣iterate下去,
做V-1次原因, 因為只有V個點,所以最長的Shortest path必定是V-1個edge, 而我們第n次更新基本上會更新到距離s第n hop的點,所以V-1次iterate足夠 基本上第一次就是更新S到第一個hop點的shortest path,第二次更新就是S到第二個hop的點的shortest path, 然後n個點最多只有n-1條edge
Floyd-Warshall Algorithm
Reference: alrightchiu
處理All Pairs shortest path的問題, 尋找每個點到其他各點的最短距離, 適用於graph不存在negative cycle時可以用, 單純有negative weight沒關係, 時間複雜度為O(V^3)
大方向的概念是針對每個點X-Y的path,每次都新加入一個中繼點, 看新增這個點會不會影響到目前既有的path, 有的話就更新, 做path relax, 例如把node Z家進來考慮, 看Path(X-Z-Y)會不會比原本Path(X-Y)小, 會的話就更新distance. 最短路徑是由較小段的最短路徑(subpath)所組成.
演算法
建議用adjacency matrix來表示,整體會比較簡單, 因為最好要能夠快速查有哪些點連到某個target node (indegree的部分)
令distance[x][y]為x-y,再目前考慮的點的set S中, 最短的距離, 初始值都是無限大
p[x][y]為x-y的shortest path下, node y的predecessor, 初始值都是-1
1. 建立兩個set S,K, K代表中繼點(尚未考慮的點), S代表目前考慮的點, 初始值S是NULL, K是所有的Node
2. 初始化時, iterate所有的edge, 如果相連就更新distance[x][y], p[x][y]
3. iterate所有點, 對於每個點, 檢查所有連接到他的點(indegree) 並做relax的部分,
例如iterate到點A, 而B,C連到A, 則檢查B連到其他點, 是否透過A會更近, 如果更近就更新distance跟p,
這個步驟要花O(V^2)的時間複雜度,
O(V) iterate所有點看那些點連到A,
O(V)對於相連的點, 要對這個相連點和其他所有點做path relax, 所以總共O(V^2)
證明, 令 \(d_{ij}^{k}\) 為考慮點集合{1…k}下, distance[i][j]的值, 假如引入某個點k,使得考慮的Set S變成{1…k}
如果k包含再i-j的最短路徑, 則 \(d_{ij}^{k}\) = \(d_{ik}^{k-1}\) + \(d_{kj}^{k-1}\), i-j經過k的最短路徑是i-k的最短路徑加上k-j的最短路徑, 而i-k, k-j的最短路徑我們再加入node k前, 就考慮過再Set s = {1…k-1}時的狀況. 所以 \(d_{ik}^{k-1}\) 就會是目前{1…k}的set中, i到k的最短路徑,k-j同理.
如果k不在i-j的最短路徑, 則 \(d_{ij}^{k}\) 會等於 \(d_{ij}^{k-1}\)
所以我們可以得出結論, 在加入新的點k後, \(d_{ij}^{k}\) = min( \(d_{ij}^{k-1}\), \(d_{ik}^{k-1}\) + \(d_{kj}^{k-1}\))
同理 predecessor也有類似的公式
\(p_{ij}^{k}\) 代表考慮node set{1..k}下i-j的shortest path, j的predecessor是誰
\(p_{ij}^{0}\) = edge(i,j) 如果i,j之間有edge相連, else 無限大
如果加入node k後 \(d_{ij}^{k}\) 沒改變, 那 \(p_{ij}^{k}\) = \(p_{ij}^{k-1}\) 反之如果加入node k後 \(d_{ij}^{k}\) 有改變, 代表i-j的shortest path有包含k這個點,此時 \(p_{ij}^{k}\) = \(p_{kj}^{k-1}\) j的predecessor變成k到j的shortest path中, j的predecessor。原本 \(p_{ij}^{k-1}\) 是i-j的shortest path下,j的predecessor, 但加入node k後, 得知現在這個path實際上不是shortest path, \(d_{ik}^{k-1} + d_{kj}^{k-1}\) 才是最短距離,i-j的shortest path變成由i-k, k-j兩段shortest path組成。 所以 \(p_{ij}^{k}\) 其實就是 \(p_{jk}^{k-1}\)
NP-complete
問題的難易度分析 動機:因為很多問題他不一定能夠用演算法想出一個很好的解,所以我們要來判斷問題的難易度避免浪費時間想一個可能沒有解的問題
decision problem: optimization problem的特化版, 判斷一個敘述是否正確(只能return true/false) 原因是這個問題沒有比optimization問題困難(可以threshold用binary search來得到optimzation的答案)
Class P: Decision problems solvable in polynomial time
Class NP: decision problems verifiable in polynomial time
Class NP-Hard: 至少比NP還難的問題(不一定是polynomial time verifiable), 而且所有NP問題都可以透過某些Polynomial time計算reduce成NP-Hard問題
CLass NP-Complete: 問題屬於NP也屬於NP-Hard(即他polynomial time verifiable而且所有NP問題都可以reduce(經過一些運算)變成這個問題), 這些問題被視為NP中最難的一群問題
如果NPC是polynomial time solvable, 則所有NP問題都可以透過Polynomial time運算變成這個NPC問題然後polynomial time解決
reduce: reduce的概念在於把一個問題A透過一些運算轉換成另一個問題B, 而問題B得出來的解會等於問題A的解, 所以我們可以把A轉成問題B, 專職在解問題B, 一旦問題B解出來了, 問題A也解出來了.舉例來說knapsack跟partition問題(給定一個array, 問有沒有辦法把它分成兩個set使2 set和相等), 我們可以輕易的把partition轉成knapsack的問題(array的值就是背包物品, sum(array)/2就是我們的背包總重限制), 這樣我們就可以專門來解knapsack, knapsack解出來, partition就解出來了
NP-Complete問題
先證明出一個問題是NPC, 接著就用reduce的方法來找出其他NPC問題. 即假設A問題為NPC, 如果我們能透過polynomial的運算把他轉成另一個問題B, 則B也是NPC (否則如果B有polynomial time解的話, 我們就可以把A的問題reduce成B解B就好, 這樣NPC問題就有polynomial time的解了)
Hamiltonian path: 一筆畫問題(可以走過所有邊依次)
Hamiltonian tour: 能夠走過所有邊一次而且結束點就是起點
四色問題
travelling sales man
- Circuit問題: 給定一個circuit(AND,OR,NOT)的連接, 總共有n個input, 是否能找到一個input使得線路output為1, 總共有2^n總可能, 要一個一個試, 目前沒polynomial解, 而且是最遠使問題, 證明所有NP問題都可以reduce成他.
- SAT: 差不多的問題, 也是n個input, 走過一連串的boolean operation(and,or,not,iff…)判斷是否能有output為1的狀況
- 3-CNF: 更嚴格的SAT, 就是把很多小括號and起來, 每個小括號裡面是一串or的statement, 一樣問有沒有一個input使最終output為1
- Clique: 給定一個graph和數字k, 能否找到graph中有k個node彼此兩兩相連
- Vertex Cover Problem, 給定graph跟數字k, 判斷能不能從中選出k個node然後這k個node所有連到的edge就等於graph的edge
- Independent-Set Problem: 給定一個graph, 找到一個Vertex Set, Set裡任兩個node在graph上不相連
- travelling sales man: 給定一個weighted graph, 找到一個路徑走過所有點然後sum最小的. decision problem變成是否能找到一個路徑走過所有點然後值小於k.
Reference
misc
Partition algorithm:
- 基本上就是選定一個pivot, 把數字比他小的放左邊,數字比他大的放右邊,所以pivot的位置會變成跟他在sorted array時一樣
- 找k-th largest element in unsorted array (O(n) on average)
- qsort(D&C + Partition)
- c++ nth_element
Reference:
Pattern matching
可以用於找一個string裡是否有substring, 或者Array裡面有沒有某個sub array pattern
範例題目: vector的sub array matching and replace
使用STL
int array[] = {1,2,3,4,1,2,3,4};
int find[] = {1,2,3};
int replace[] = {7,8,9};
auto it = array.begin();
while(true) {
it = search(it,array.end(),find.begin(),find.end());
if(it == array.end()) break;
it = copy(begin(replace), end(replace), it);
}
Time complexity: naive approach -> O(len(array) * len(find))
boyer Moore algorithm
Reference: Geek for geeks
TBD