Information Theory
30 April 2019
好讀版: https://hackmd.io/@NCGXxkNfR2WNISqcwagt4Q/rk68MWMYB
Computational secure
解決問題最佳的演算法仍需要很久的時間,攻擊者有limited resources(但可能很大) 通常會把問題reduce成某些很難、沒有快速解法的問題,如RSA是立基於質數分解的問題
Unconditional secure
= perfectly secure 即使攻擊者有一大堆資源,也沒辦法破壞密碼系統
Bayes’ Theorem
\(P(X \|Y) = \dfrac{P(Y \|X)*P(X)}{P(Y)}\)
cryptography definition
P : plaintext
C : cipher
ek() : encryption with key k
dk() : decryption with key k
P(C = c ) = \(\sum{P(P=m)*P(e_k(m) = c)}\)
p(P=m | C=c ) = \(\frac{p(C=c \|P=m)*p(P=m)}{p(C=c)}\)
= \(\frac{p(P=m)*p(d_k(c)=m)}{p(C=c)}\)
因此可以知道看到cipher c,可以推斷出來自plaintext m的機率,等於看到ciphertext後會洩漏一些plaintext的資訊
Perfect Secrecy
P(P=m \|C=c) = P(P=m)
P(C=c \|P=m) = P(C=c)
plaintext,ciphertext是獨立事件,也就是說看到ciphertext不會知道任何plaintext的資訊
Shannon’s theory
假設(P,C,K,\(e_k(.)\),\(d_k(.)\)) 且 #P = #C = #K, plaintext,ciphertext,key數量一樣 則這個系統是perfect secrecy iff 每個key被使用的機率都是1/#K,而且每個 m \(\in\) P, c \(\in\) C,都是透過一個unique的key k, \(e_k(m)=c\)
正向Proof(perfect secrecy ->)
\(e_k(m)=c\), k is unique
對任何的一個plaintext m \(\in\) P ,每個ciphertext我們都有一把key k 使 \(e_k(m) = c\) 故 #C \(\leq\) #K 因為題目假設#P = #C = #K 故 #C = #K 所以不可能存在兩把key\(k_1,k_2\)使 \(e_{k1}(m) = e_{k2}(m) = c\)
every key has equal probability 1/#K
因Perfect Secrecy
p(P=\(m_i\) |C=c) = p(P=\(m_i\))
p(P=\(m_i\)) = p(P=\(m_i\) |C=c)
= \(\dfrac{p(C=c \|P=m_i)p(P=m_i)}{p(C=c)}\)
= \(\dfrac{p(K=k_i)p(P=m_i)}{p(C=c)}\)
故得 p(C=c) = p(K=\(k_i\)),而所有key \(k_i \in K\) 都能這樣推倒,所以這樣的證法做n(key的次數)遍,得
np(C=c) = 1, 因\(\sum{k_i} = 1\)
得p(C=c) = \(\frac{1}{n}\) = p(\(k_i\))
反向proof(->perfect secrecy)
在 #K = #C = #P的crypto system中 if每把key被使用的機率都是1/K且 使\(e_k(m) = c\)的k都是unique的 則 p(P = m | C = c) = p(P = m)
p(C = c ) = \(\sum{p(k = K)p(P = d_k(c))}\)
又p(k) = \(\dfrac{1}{K}\)
p(C = c) = \(\sum{p(P=d_k(c))/K}\) 又條件中 對每個m有一個獨特的key k使,所以在知道k,c的時候,只有一個p能符合\(d_k(c)\) \(e_k(m) = c\) \(\sum{p(P=d_k(c))}\) = \(\sum{p(P=m)}\) = 1
故 p(C=c) = \(\dfrac{1}{K}\)
如果c = \(e_k(m)\) 再決定c,m時,只有一把key符合該條件,機率為\(\dfrac{1}{K}\)
p(C = c \ | P = m) = p(K = k) = \(\dfrac{1}{K}\) = p(C = c)
利用貝氏定理 p( P = m | C = c) = \(\dfrac{p(C = c \| P = m)p(P = m)}{p(C = c)}\) = p(P = m)
Sample of perfect Secrecy
shift cipher
P = K = C = 26 \(e_k(m) = (m+k)%26\) 如果plaintext只有一個字元,那就是perfect secrecy, p(k = K ) = 1/k
one-time-pad
problems:
- key cannot be reused
- key should have length equals to the plaintext 這些都是要有著一個前提:P = K = M, key長度要跟plaintext依樣,而且還不能重複使用,不然one-time-pad就可以xor密文或密文xor明文,這樣可以得到兩個plaintext的比較或者key。 而這麼長的key,每個plaintext都要用不同的,會造成key distribution的問題
Solution
- 目前密碼系統都是一把key重複使用
- key space原則上遠小於plaintext space, cipher space, key space能到512 bits就很了不起了,最多也只有到4096 bits
- 使用information theory來分析密碼系統的安全性
Information theory
Entropy
令X為事件 X = {\(x_1,x_2...x_n\)},分別發生機率為P, P={\(p_1,p_2...p_n\)} H為熵,即亂度,以下為H的特性
- H(X)最大時為 \(\forall p_i = p_j = \dfrac{1}{n}\)。
- H(X) \(\geq\) 0
- H(\(x_1,x_2...x_n\)) \(\leq\) H(\(x_1,x_2...x_{n+1}\))
- Let p = \(p_1+p_2...+p_n\), q = \(q_1+q_2...+q_n\), p+q = 1, 則
- H(\(p_1,p_2...q_1,q_2..q_n\)) = H(p,q)+pH(\(p_1/p,p_2/p...p_n/p\)) + qH(\(q_1/q,q_2/q...q_n/q\))
H = -\(\sum{p_ilog_2p_i}\) 忽略\(p_i\) = 0的狀況
Information
Information I of event E with probability p:
I(E) = \(-log_2(p)\)
Concolusion
從上述公式可得知,H其實就是Information的期望值,所以loss of entropy = gain of information
Jensen’s inequality
\(a_i\) > 0, \(\sum{a_i} = 1\)
if \(x_i > 0\) then
\(\sum{a_ilogx_i} \leq log\sum{a_ix_i}\)
equality holds when \(x_1 = x_2... = x_n\)
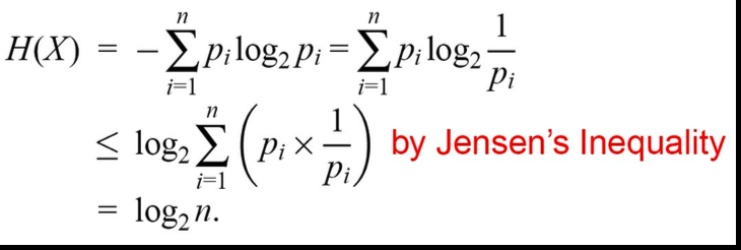
Joint Entropy
Event X = {\(x_1,x_2,x_3...\)}, Event Y = {\(y_1,y_2,y_3...\)} \(r_{ij}\) = p(\(X = x_i, Y = y_j\))
H(X,Y) = \(\sum{\sum{r_{ij}log(r_{ij})}}\)
H(x,y) \(\leq\) H(x) + H(y)
等號成立於X,Y event為獨立事件 直覺思考,x,y會互相影響,導致有些事件不可能同時發生,所以亂度降低,反之如果將兩個事件分開,那所有x,y組合的事件就有可能產生
Conditional Entropy
\(H(X \| Y=y_j\)) = -\(\sum{p(X=x_i \|y_j)logp(X=x_i \|y_j)}\)
\(H(X \|Y) = -\sum{p(Y=y_j)H(X \|Y=y_j)}\)
H(X,Y) = H(X |Y) + H(Y)
H(X |Y) \(\leq\) H(X) 等號成立於X,Y為獨立事件
Information & Entropy
I(X |Y) = 0 iff X,Y是獨立事件
I(X |Y) = I(Y |X)
I(X |Y) = H(X) - H(X |Y) 看到Y少掉的X的亂度 = X |Y洩漏的info
Entropy and Cryptography
H(C |P,K) = 0 H(P |C,K) = 0
H(P,K,C) = H(C |P,K) + H(K,P) = H(P,K) = H(P) + H(K)
H(K,C,P) = H(P |C,K) + H(C,K) = H(C ) + H(K)
故H(K) + H(P ) = H(C,K)
Key Equivocation
I(K |C) = H(K) - H(K |C) 看到C少掉的K的亂度 = K |C洩漏的info
H(K |C) = H(K,C) - H(C ) = H(P )+H(K)-H(C ) 意義:看到Cipher後的亂度
I(K |C) = H(K) - H(K |C) = H(K) - (H(K,C) - H(C )) = H(C ) - H(P )