Logistic regression & classification
02 May 2020
Generative Model & Discriminative Model & Discriminant Function
- Generative Model: 計算event X屬於各個class的機率:
P(C1|x),並把x歸類在機率最高的那個class - Discriminative Model: 類似Generative model,用條件機率,但不單純只看input的分布狀況,也不考慮P(x,y)的狀況,利用學習現有資料來做盼度ㄢ。例如某種值有較高機率屬於某種class之類的
- Discriminant Function: 直接input event,經過一些運算後,直接output class,即該event屬於哪個class,跟機率無關。
Classification Method
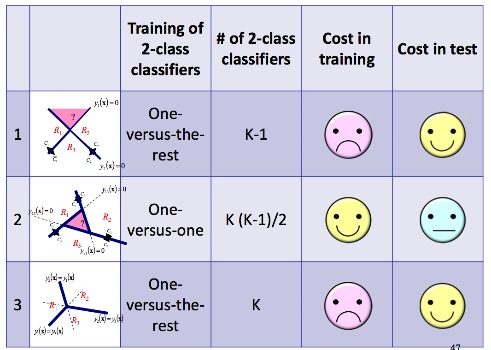
One-versus-the-rest
總共需要k-1個model,每個model只判斷屬不屬於該class,是binary classification,例如Line 1只判斷event屬於class 1或不屬於class 1,所以k個class總共需要k-1條,都不屬於的event就歸類在最後一個class。
但這種方式會產生某些event同時屬於兩種class。
One-versus-one
K個class的分類時,總共需要 K(K-1)/2個model,基本上每個model也是binary classification,判斷event屬於class A還class B,所以K個class總共有 \(c_2^k\) 總組合。
每來一筆新的event,就輸入到所有model,用投票方式判斷屬於哪個class。但依樣會有多個class可能會有一樣的票數的問題。
One-versus-the-rest with Discriminant
K個class有K個model,基本上每個model就是discriminant,直接輸出event屬於哪個class。但這個training難度很高
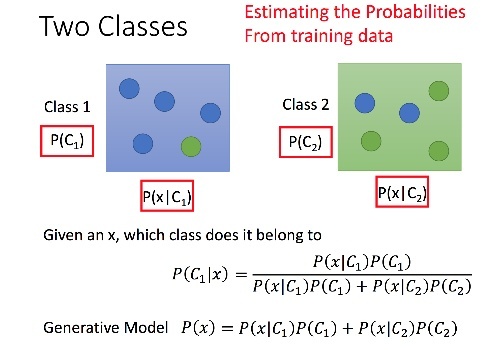
Probalistic Genrative model
就是貝氏定理的應用,如下圖,判斷某x屬於哪個class就算 P(C|x),即算已知是x,則x從class1還是class2出來的機率哪個高,作法就是把label的點算mean,variance,就可以求出個別class的高斯分佈,對每個testdata做下述公式。
if P(C1|x)>0.5 x屬於Class1
else x屬於Class2
- 作法:
- 找出一個函式 f(C1|x) 給定一個data x函式能夠輸出屬於class1,class2的個別機率(可以用高斯分佈、白努力分佈,看data狀況)
- 找出mean,covariance使training data分類上屬於自己class的機率最高的值
- 帶入testing data判斷屬於哪個class
- Modify: 按照上述算法,會得到class1,class2個別自己的mean,variance,修改算法是不同的class共享一個variance,若有個別的variance則參數多,容易overfit,所以不同class共用variance來避免參數過多
假設train data有140筆,79筆data屬於class1,61筆屬於class2
\(\sigma\) =\(\frac{79}{140}\) \(\sigma_1\) +\(\frac{61}{140}\) \(\sigma_2\)
\(\sigma_1\)\(\sigma_2\)是class1,class2個別的variance,\(\sigma\)為修改後的covariance,class1,class2都用這個covariance
- Naive bayse classification
上述的方法求出來的是covariance,會有不同feature之間的covariance,如果假設每個feature是獨立事件,那公式可以變成
P(\(C_1\)|x) = P(\(x_1\)|\(C_1\)) * P(\(x_2\)|\(C_1\)) * P(\(x_n\)|\(C_1\))
即算個別feature屬於那個class的機率然後相乘,但效果不好,因為feature間很難是獨立事件
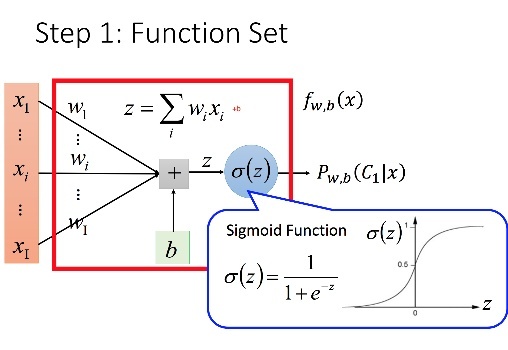
Perceptron learning
基本上就是學神經元的部分,把值丟進去做運算,數字大於一定的條件就會output 1,其餘output 0之類的。
因此可以用這個來做classification,通常配合sigmoid的方式,因為他就是類似數字大於一定條件output 1 其餘 0
這種模型能避免那種很大的noise把整個分割線在training時被拉走,因為error在大,他造成的結果頂多就是1個classification錯誤,不會因為error值很大而對新的weight有很大影響。
Training方式就是一次拿一個點,如果他錯誤就用該點update weight,如果該點判斷正確,就continue
\(w^{t+1} = w^t - \eta \nabla E_{p}(w)\)
\(w^{t+1} = w^t + \eta x_{n}t_{n}\)
Sigmoid
下式\(\sigma(z)\)就是sigmoid function,函示圖形為sigmoid function的圖形,可知在z很大及很小時,sigmoid function趨緩
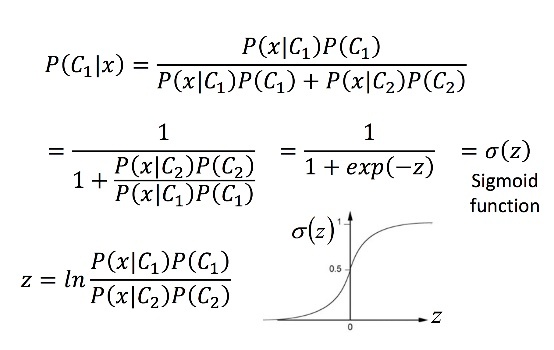

由複雜證明可得 P(\(C_1\)|x) = \(\sigma(wx+b)\) ,w,b算法在上圖
Logistic Regression(分類)
\(P_{w,b}\)(\(C_1\)|x) = \(\sigma(z)\) w,b為參數
z = wx+b
\(\sigma(z)\)=\(\frac{1}{1+exp(-z)}\)
- Loss Function
Loss function的先決條件是要可以微分才能做gradient Descent把loss縮小
\(f_{w,b}\) = \(P_{w,b}(C_1\) |x),即function是判斷某筆data屬於class 1的機率
| \(x_1\) | \(x_2\) | \(x_3\) |
|---|---|---|
| class1 | class2 | class1 |
L(w,b) = \(f_{w,b}\)(\(x_1\))(1-\(f_{w,b}\)(\(x_2\)))\(f_{w,b}\)(\(x_3\))
L : 產生x1,x2,x3是這樣值的機率(所以要越大越好)
因\(x_2\)屬於Class2,所以要1-屬於Class1的機率
argmaxL(w,b) = argmin -lnL(w,b)
-lnL(w,b) = -ln\(f_{w,b}\)(\(x_1\)) - ln(1-\(f_{w,b}\)(\(x_2\))) - ln\(f_{w,b}\)(\(x_3\))
-ln\(f_{w,b}\)(\(x_1\)) = ylnf(\(x_1\)) + (1-y)lnf(\(x_1\))
故當class=1時 會計算ylnf(\(x_1\))這項,當class=2時(label=0)會計算(1-y)lnf(\(x_1\))這項
用square loss即(x-1)的平方這種做法有可能會導致x太大時loss太大
故通常會取sigmoid的方式把輸出值壓小,避免x太大
因此Logistic Regression使用Cross Entropy

-lnL(w,b)越小越好
- Logistic Regression與Linear Regression差別

- gradiant descent: 算出最適合的w,b,對-lnL(w,b)做對每個\(w_i\)的偏微分,使用連鎖率

Genrative Discriminative model
| Generative model | Discriminative model |
|---|---|
| 腦補 | train |
| 直接算出mean,variance | 用gradiant descent算出mean,variance |
| data少時可能有幫助 | data數量多時用 |
Softmax(於Multiclass classification)
使輸出直加起來為1,在multiclass classification中,每個class都有自己的w,b,把data帶入後算出屬於每個class的機率再取exponential(強調機率大的class)後再做softmax,得到data屬於三個class的機率(此時屬於3個class機率和為1)
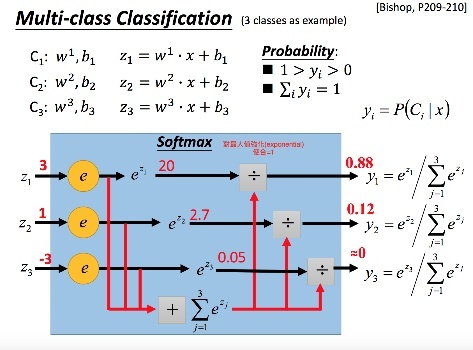
softmax輸出值後在與最後的label data做cross entropy(label data是one hot encoding)

Logistic Regression的極限
下圖這種類型找不到分類法把它分好
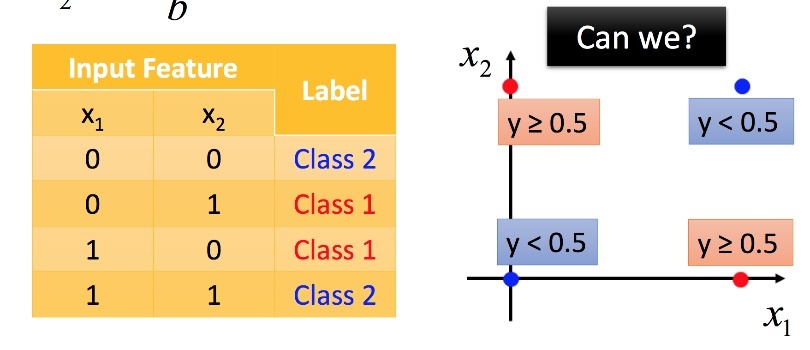
解法:Deep Neural Network,前面幾層layer當作feature transformation,把feature轉成最後一層能做分類的feature